Epistemology
Bush and Mosteller Learning Curve
This section was mostly taken from Paul W. Glimcher1 paper in PNAS[1]
This very general idea of Conditional learning, was first mathematically formalized when Bush and Mosteller[2], 24) proposed that the probability of Pavlov's[3] dog expressing the salivary response on sequential trials could be computed through an iterative equation where
In this equation, Anext_trial is the probability that the salivation will occur on the next trial (or more formally, the associative strength of the connection between the bell and salivation). To compute Anext_trial, one begins with the value of A on the previous trial and adds to it a correction based on the animal's experience during the most recent trial. This correction, or error term, is the difference between what the animal actually experienced (in this case, the reward of the meat powder expressed as Rcurrent_trial) and what he expected (simply, what A was on the previous trial). The difference between what was obtained and what was expected is multiplied by α, a number ranging from 0 to 1, which is known as the learning rate. When α = 1, A is always immediately updated so that it equals R from the last trial. When α = 0.5, only one-half of the error is corrected, and the value of A converges in half steps to R. When the value of α is small, around 0.1, then A is only very slowly incremented to the value of R.
What the Bush and Mosteller[4][5] equation does is compute an average of previous rewards across previous trials. In this average, the most recent rewards have the greatest impact, whereas rewards far in the past have only a weak impact. If, to take a concrete example, α = 0.5, then the equation takes the most recent reward, uses it to compute the error term, and multiplies that term by 0.5. One-half of the new value of A is, thus, constructed from this most recent observation. That means that the sum of all previous error terms (those from all trials in the past) has to count for the other one-half of the estimate. If one looks at that older one-half of the estimate, one-half of that one-half comes from what was observed one trial ago (thus, 0.25 of the total estimate) and one-half (0.25 of the estimate) comes from the sum of all trials before that one. The iterative equation reflects a weighted sum of previous rewards. When the learning rate (α) is 0.5, the weighting rule effectively being carried out is an exponential series, the rate at which the weight declines being controlled by α.
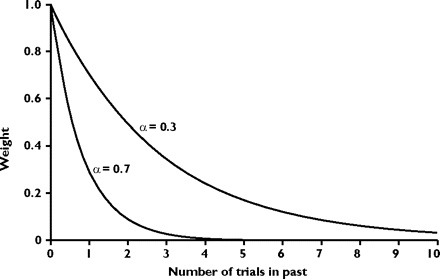
When α is high, the exponential function declines rapidly and puts all of the weight on the most recent experiences of the animal. When α is low, it declines slowly and averages together many observations, which is shown in Fig. 1.
Fig 1: “Weights determining the effects of previous rewards on current associative strength effectively decline as an exponential function of time”[6].
The Bush and Mosteller equation was critically important, because it was the first use of this kind of iterative error-based rule for reinforcement learning; additionally, it forms the basis of all modern approaches to this problem. This is a fact often obscured by what is known as the Rescorla–Wagner model of classical conditioning[7]>. The Rescorla–Wagner model was an important extension of the Bush and Mosteller approach to the study of what happens to associative strength when two cues predict the same event. Their findings were so influential that the basic Bush and Mosteller rule is now often mistakenly attributed to Rescorla and Wagner by neurobiologists.
References
- ↑ Glimcher, P. W. (2011). Understanding dopamine and reinforcement learning: the dopamine reward prediction error hypothesis. Proceedings of the National Academy of Sciences of the United States of America, 108 Suppl (Supplement_3), 15647–54.
- ↑ Bush RR, Mosteller F (1951) A mathematical model for simple learning. Psychol Rev 58:313–323
- ↑ Pavlov IP (1927) Conditioned Reflexes: An Investigation of the Physiological Activity of the Cerebral Cortex (Dover, New York).
- ↑ Bush RR, Mosteller F (1951) A mathematical model for simple learning. Psychol Rev 58:313–323
- ↑ Bush RR, Mosteller F (1951) A model for stimulus generalization and discrimination. Psychol Rev 58:413–423.
- ↑ Schoenbaum G, Roesch MR, Stalnaker TA, Takahashi YK (2009) A new perspective on the role of the orbitofrontal cortex in adaptive behaviour. Nat Rev Neurosci 10:885–892.
- ↑ Rescorla RA, Wagner AR (1972) in Classical Conditioning II: Current Research and Theory, A theory of Pavlovian conditioning: Variations in the effectiveness of reinforcement and nonreinforcement, eds Black AH, Prokasy WF (Appleton Century Crofts, New York), pp 64–99.