Epistemology
|
This page is a stub. It is not ready for publication and is used to aggregate information about a subject. You can add further reading and add information to the page. If you want to prepare this page for publication please consults with the creator of this page. |
|
This page was writen by a non-English speeking writer. Please help us improve the quality of the paper.Tal Yaron 14:08, 20 February 2013 (IST) |
Contents
The Foundations of Knowledge
The phenomenological cage
Deliberation is a process of thoughtfully weighing options before making a decision. Yet in order to choose among the available options, we have to agree on the options available to us, and theןir outcomes. But many times we find ourselves in disagreement about the options or the ways the world behave. These disagreements are the results of differences in our understanding of how the world works. So in order to be able to better understand why we perceive the world differently, I suggest we have to understand how our knowledge is built, and why it is different from person to person. This Page will try to explain how knowledge is built and why we perceive the world differently.
To explain knowledge, I will suggest that knowledge is a thing that is being used to understand, explain, predict and manipulate the inputs that come from the senses.
Thouse inputs that come from our senses, whether outer senses like smell, vision, hearing, touch, wormth, etc. or from our inner senses like therst, hounger, love, hate, etc are all will be called the phenomena. Phenomena, with correspondance to Kant's philiosophy, is our senses expriences.
Through the usage of knowledge we try to understand our surroundings and inner feelings, but we have a an unobservable barriar to the surrounding or even our inner selves. We have no access to the surrounding itself. All our knowledge about the "surrounding" comes from our senses. We have pehnomena, but no access to the thing that creates the expreinces. For more than 2500 years of epistemology, nobody had found a reliable way to establish a relations between perception and the “surrounding”. To demonstrate the problem of the relations between knowledge and the surronding, we may use the thought experiment of the “brain in a vat”. In this thought experiment, you are asked to find a reliable way to know if you really exists as you perceive it, or you are actually a brain in a vat, which gets it's sensory inputs from a computer, that simulate the perceived world.
Till today nobody was able to find a reliable answer to this question. Philosophers sometime suggest that Hillary Putnaham had found a way, but his conclusions say otherwise. He concluded that we cannot distinguish between realty and virtual experience[1].
Therefore, we have to set for now an axiom that says:
- “We do not know the relation between our knowledge and the inner or outer-world”. Or in Kant's methodology, we cannot know the noumenon.
The only thing we can say is that we percive. How this perception is constructed, I will suggest later own in this paper. as a result of our inability to go beiond our perceptions, I will call this principle "The phenomenological cage principle".
Axioms of Knowledge
The Phenomena
Kant described the inputs from the senses as “phenomena”.
Propensities in the phenomena
Knowledge is about tring to predict the phenomena. In the effort to predict I will suggest that we use the axiom that says that the phenomena are inputs from our senses which gets inputs from some source (Which Kant named neumena, or the thing in itself). We can "feel" the neumena by the following mechanism: When there is no input from the neumena, the phenomena will be random or blank, and when the neumena is interacting with the senses, it will create some propensities in the otherwise random or blank phenoemna[2]. It will suggest that the neumena will create some order in the phenomena.
This axiom may not describe the real relations between the phenomena and the neumena (If such exists), but it helps understand the way our system of creating knowledge works. The system assumes that such relation between phenomena and neumena exists, and all the following calculations will work based on this assumption.
Spesific Phenomena
I will also assume that these propensities in the phenomena creates destinguished specific phenomena. the destinguishable phenomena may be specific smells, sounds, feelings, touch, tastes etc. I will call it Destinguished Specific Phenomena (DSP).
Memory
I will aslo assume that the mind can store past DSPs for a while.
Similarity and Induction
In the memory when a combination of two or more DSPs reoccurs, a connection in the memory is formed. For instance, if a smellx occur with specific soundy, and this combination reoccur several time while still in memory, then the memory might assume that the combination is eminent. This will be called induction, because from some limited set of co-occurrence, the mind assume that this co-occurrence will always reoccur. Of course the induction might not stand the next occurrence of either one of the DSPs. We will deal with this later.
See also the problem of identity
Simplicity
The induction between two DSPs might be very simple. They may be linked directly. For instance, a sound of a broken glass may be directly connected to a look of a braking glass, because the Neumann that creates these two specific DSPs, is always affect the phenomena in the same pattern. But it can be connected in more complex ways, for instance the Neumann that creates these two DSPs may be a computer that creates a breaking sound, whenever he creates a visual DSP of breaking glass. Because the Neumann can change its effect on DSPs, the induction may describe well the relation between the DSPs until sometime in the comming observations, and it may be not describe the relation in the future[3]. The reason to choose the simplest induction is because the number of available possible relations between a sound and a breaking glass are infinite. Therefore for reasons of effective storage, we will use to use the simplest induction which is the minimum usage of information to describe maximum relations of DSPs. In our case it might be "All breaking glasses has this specific sound".
Refutation
For the sake of economic usage of memory storage we will assume the simplest inductions between DSPs. Yet, in the coming phenomena we may notice that the induction does not describe well the relation between the DSPs. We might find that although we have the induction "smellx always come with soundy", we might notice that in the coming observations soundy do not follow smellx. This will cause refutation of the induction, and we will have to try to create a new induction or forget the refuted induction. If we want to suggest a more complex induction we may look at our stored relations between DSPs, and see that when smellx was not followed by soundy, a touch-feelingz did occur just before the appearance of smellx. Therefore we may suggest the following induction " smellx always come with soundy unless touch-feelingz occur just before smellx".
From the sets of stored memory about realtions of DSPs we may suggest many different inductions that may describe the occurence of DSPs, but yet again for the sake of economical storage, it will be better to use the simplest induction possible to describe maximum observable relations between DSPs.
This Process of suggesting induction, refutatios and resuggesting a more complex induction, is part of the continued process of creating knowledge.
Structures of Knowledge
Mental Objects
Senssory Mental Objects
Somtimes the brain finds several connections between diffrent DSPs, that come toghther. When several connections are reoccuring they form a cluster of inductions. I call this cluster of induction a Mental Object (MO). It is an object that sotres many inductions that relate to eache other. For instance a specfic smell may come always when specific shape and specifice color and specific feeling. A smell of an apple may come with a shape of an apple, a color of an apple and a taste of an apple. This cluster of inductions will create for us a femiler object that when ever we observ one of it's DSP, we will assume that all other DSPs will appaer also. If we will also hear the same name ("apple") every time we will see some of the connected appreances, we will also give him a name: "apple"[4] that will be part of the mental object.
To be continued...
Mental Objects are compused of inductions and as every induction in the phenomenological cage, they should be put to a test. Therefore MOs may change and reconstracted. For instance, all the apples we have seen so far were red. Sudenly I see a shape of an apple, I smell a smell of an apple and it has a feeling of an apple, but it's color is green and it's taste is diffrent. What is it? I have expreinced a refutation of my expected apperances by the old MO:apple. As in every induction, when it is refuted, we have to find new set of inductions that will describe all appreance we have seen so far. The posiblities to describe all phenomena is infinte, and again we will look for the simplest sets of connections that will describe all abservations. One simple rearngments will be to say that the old observations and the new observationare are two diffrent objects. Another simple reconstruction will be to say that all my observation relating this MO:apple are of the smae object but diffrent of kinds. In the former the connection to red and sweet (This is the taste of the red object), will be on mental object, while the the green and the soure will be another object. Both objects have the same shape and the the same touch and the same smell, but different colors and tastes. In the later, they are all apples, and apples have purticular shape, feeling and smell, but there is a kind of red-sweet appels and there is a kind of green-sour appels. of course there may be other ways to to reconstruct mental objects. We can say that all apples are red, but sombody painted and weetend this last observation of an apple, or this was an accident, freak of nature and so on.
To decide ifbetween alternatives we may need some more avidance. Further evidance may suggest that we should divied it to two diffrent mental objects. For instance if our theoris will be sufficiantly developed to the point when we recognize a "DNA" thus we may find that they have a DNA linage that is very diffrent, and because we defined DNA as an assntial proprtie of a leaving object, we may decide that they are two diffrent mental objects.
Deductions
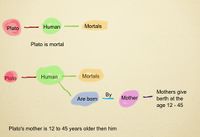
Mental Objects construct our understanding of the world. When we reason, we can go along the lines of connected MOs. For instance, humans have many inductions. We know that they have two legs, two arms, they leave up to 120 years, and in the meanwhile they breath, born and die, and many other inductions (mistakenly called proprties). We also know (or conjecture) that Socrates was human, and as such he has all the inductions of the MO:humans.
When we use the clasical sylogism "Socrats was human, all humens are mortal, therfore Socrates is mortal" we go along the lines that connect the MOs. By this mechanism we may say that Socrates was also born. If we want to speculate how old was his mother when she gave birth to Socrates we need some other inductions and mental object. we need to conjectures in what ege women can give birth (age 12-45), and that humans are born by womens and that that woman is his mother. Therefore we can conculde that Socrates was born when his mother was at the age of 12-45, and we therfore conclude that his mother is 12-45 years older then Socrates.
|
This section needs more clarifications. Please explein: |
Imaginary Mental Objects
Some times we have gaps between our mental objects. These gaps usually puzzle us and we look for an explanation or some intermediate MO that will closes the gap. Therefore we invent an unseen MO to bridge the gap. When we invent the bridging MO, we usually imagine it and we do not get if from phenomenological intervals (when we will further research, we will see that all MOs are imaginary mental objects), therefore we will call it Imaginary Mental Object or iMO, while the objects obtained from phenomenological intervals will call Sensory Mental Objects(sMO).
For instance, when the ancient looked upward and saw the sun travels through the skies, the where puzzled. The knew that every object that is traveling need something to pull or to thrust it, yet the sun seems to move without a mover. To solve it, they invented a "story" or a mental object that was missing. They told their hearers that the sun is pulled by invisible horses. The invisible horses where their iMO that bridged the gap.
We use iMOs more then we recognize naturally. All our theories and especially the scientific theories are built of networks of iMOs. We only seldom see directly our iMOs. For instance iMO:atoms was talked about for more then 200 years in the modern science. Yet not until recently people did not observe atoms. And even today when we "see" atoms it is through very complicated theories constucted into the scientific observation tools. We cannot observe atoms directly,and therefore atoms will stay iMOs.
People who do not engage epistemology are not awere of the extant of our usage of iMOs. Hume was probably the first thinker that showed the we take for granted things we do not see. He demonstrated in his book An Enquiry Concerning Human Understanding[5], that cause and effect are not to be observed directly, yet people use them as though they are real enteties. God is iMO, and also The force of gravity, and even the state is an iMO (Have any of you ever seen a state?).
Advance Asspects of Knowledge
Simple and Complex Mental Objects
Simple MOs is a MOs which are only constructed from inductions. Complex MOs are MOs which are constructed from sub-MOs, and therefore creates mechanism to the Complex MO. For instance, a simple MO may be "the earth attracts heavy bodies" and a complex MO may be "between particles with masses there is a flux of gravitons that attract the masses according to the low of gravity. Therefore any body with mass will attract any other body with mass, due to the attraction of the gravitons". When we try to explain a MO, we try to make it complex. Sometimes we are unable to further explain a MO, and therefore we will call the Axioms. But it is possible that in the future, when we gain more undersanding we may be able to explain the basic MOs and make them comlex. hence, explanation' is the procees of making a MO more coplex.
Other Asspects of Knowledge
Bush and Mosteller Learning Curve
This section was mostly taken from Paul W. Glimcher1 paper in PNAS[6]
This very general idea of Conditional learning, was first mathematically formalized when Bush and Mosteller[7], 24) proposed that the probability of Pavlov's[8] dog expressing the salivary response on sequential trials could be computed through an iterative equation where
In this equation, Anext_trial is the probability that the salivation will occur on the next trial (or more formally, the associative strength of the connection between the bell and salivation). To compute Anext_trial, one begins with the value of A on the previous trial and adds to it a correction based on the animal's experience during the most recent trial. This correction, or error term, is the difference between what the animal actually experienced (in this case, the reward of the meat powder expressed as Rcurrent_trial) and what he expected (simply, what A was on the previous trial). The difference between what was obtained and what was expected is multiplied by α, a number ranging from 0 to 1, which is known as the learning rate. When α = 1, A is always immediately updated so that it equals R from the last trial. When α = 0.5, only one-half of the error is corrected, and the value of A converges in half steps to R. When the value of α is small, around 0.1, then A is only very slowly incremented to the value of R.
What the Bush and Mosteller[9][10] equation does is compute an average of previous rewards across previous trials. In this average, the most recent rewards have the greatest impact, whereas rewards far in the past have only a weak impact. If, to take a concrete example, α = 0.5, then the equation takes the most recent reward, uses it to compute the error term, and multiplies that term by 0.5. One-half of the new value of A is, thus, constructed from this most recent observation. That means that the sum of all previous error terms (those from all trials in the past) has to count for the other one-half of the estimate. If one looks at that older one-half of the estimate, one-half of that one-half comes from what was observed one trial ago (thus, 0.25 of the total estimate) and one-half (0.25 of the estimate) comes from the sum of all trials before that one. The iterative equation reflects a weighted sum of previous rewards. When the learning rate (α) is 0.5, the weighting rule effectively being carried out is an exponential series, the rate at which the weight declines being controlled by α.
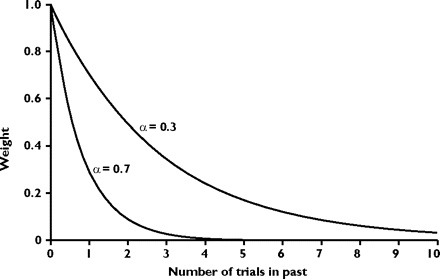
When α is high, the exponential function declines rapidly and puts all of the weight on the most recent experiences of the animal. When α is low, it declines slowly and averages together many observations, which is shown in Fig. 1.
Fig 1: “Weights determining the effects of previous rewards on current associative strength effectively decline as an exponential function of time”[11].
The Bush and Mosteller equation was critically important, because it was the first use of this kind of iterative error-based rule for reinforcement learning; additionally, it forms the basis of all modern approaches to this problem. This is a fact often obscured by what is known as the Rescorla–Wagner model of classical conditioning[12]>. The Rescorla–Wagner model was an important extension of the Bush and Mosteller approach to the study of what happens to associative strength when two cues predict the same event. Their findings were so influential that the basic Bush and Mosteller rule is now often mistakenly attributed to Rescorla and Wagner by neurobiologists.
References
- ↑ Putnam, H. (1981): "Brains in a vat" in Reason, Truth, and History, Cambridge University Press; reprinted in DeRose and Warfield, editors (1999): Skepticism: A Contemporary Reader, Oxford UP
- ↑ Popper, K. (1997). World of Propensities (p. 60). Thoemmes Press.
- ↑ Goodman, N., & Putnam, H. (1983). Fact, Fiction, and Forecast, Fourth Edition (p. 160). Harvard University Press.
- ↑ Wittgenstein, L. (1973). Philosophical Investigations (3rd Edition) (p. 250). Pearson.
- ↑ Hume D. (1748) An Enquiry Concerning Human Understanding
- ↑ Glimcher, P. W. (2011). Understanding dopamine and reinforcement learning: the dopamine reward prediction error hypothesis. Proceedings of the National Academy of Sciences of the United States of America, 108 Suppl (Supplement_3), 15647–54.
- ↑ Bush RR, Mosteller F (1951) A mathematical model for simple learning. Psychol Rev 58:313–323
- ↑ Pavlov IP (1927) Conditioned Reflexes: An Investigation of the Physiological Activity of the Cerebral Cortex (Dover, New York).
- ↑ Bush RR, Mosteller F (1951) A mathematical model for simple learning. Psychol Rev 58:313–323
- ↑ Bush RR, Mosteller F (1951) A model for stimulus generalization and discrimination. Psychol Rev 58:413–423.
- ↑ Schoenbaum G, Roesch MR, Stalnaker TA, Takahashi YK (2009) A new perspective on the role of the orbitofrontal cortex in adaptive behaviour. Nat Rev Neurosci 10:885–892.
- ↑ Rescorla RA, Wagner AR (1972) in Classical Conditioning II: Current Research and Theory, A theory of Pavlovian conditioning: Variations in the effectiveness of reinforcement and nonreinforcement, eds Black AH, Prokasy WF (Appleton Century Crofts, New York), pp 64–99.